Factores
Se llama factores o divisores de una expresión algebraica a las expresiones algebraicas que multiplicadas entre sí dan como producto la primera expresión.Así, multiplicando a2 por a+b tenemos :
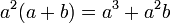
Igualmente:
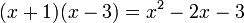
luego, (x+1) y ( x−3) son factores de x2−2x−3
Definición
Factorizar una expresión algebraica es convertirla en el producto indicado de sus factores. |
Factorizar un monomio
Los factores de un monomio se pueden hallar por simple inspección. Así, los factores de 21a2c3 son: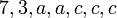
Por tanto:
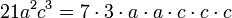
Factorizar un polinomio
No todo polinomio se puede descomponer en dos o más factores distindos de la unidad, pues del mismo modo que, en Aritmética, hay números primos que sólo son divisibles entre ellos mismo y por la "unidad", hay expresiones algebraicas que sólo son divisibles por ellas mismas y por la "unidad", y que, por tanto, no son el productos de otras expresiones algebraicas. Así a+b no puede descomponers en dos factores distinos de 1 porque sólo es divisible por a+b y por 1.Prueba general de factorización
En cualquiera de los casos que estudiaremos, la prueba consiste en multiplicar los factores obtenidos, su producto tiene que ser igual a la expresión que se ha factorizado.Ejemplo:
Al factorizar la expresión
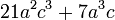 se obtiene:
se obtiene: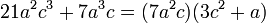
La prueba consiste en multiplicar los factores obtenidos. El resultado deberá ser la expresión original:
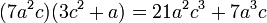

No hay comentarios:
Publicar un comentario